Question

The box of a well-known breakfast cereal states that one ounce of the cereal contains 113 Calories (1 food Calorie = 4186 J). If 1.79% of this energy could be converted by a weight lifter's body into work done in lifting a barbell, what is the weight of the heaviest barbell that could be lifted a distance of 1.90 m?

Answer 1

`m=454.73 kg`

Step-by-step explanation:

To convert the energy of the cereal to know the weight:

`m*g*h=Q'`

`Cal=0.0179*113 Cal=2.0227Cal`

`Q'=2.0227Cal*(4186J)/(1Cal)`

`m*g*h=8467.02J`

`m*g=(Q')/(h)=(8467.02J)/(1.90m)`

`m*g=4456.33 N`

Supuse the gravity as a g=9.8m/s^2

`m=(4456.33N)/(9.8m/s^2)`

`m=454.73 kg`

Answer 2

4456.33N

Step-by-step explanation:

Let the energy converted by the lifter's body into work done be E.

The work done in lifting the barbell is against gravity and it is given by equation (1);

`work done=mgh..................(1)`

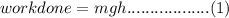
where m is the mass of the barbell, g is acceleration due to gravity and h is the vertical distance (height) through which it is lifted. Hence by the principle of energy conversion as specified by the problem we could write the following equation;

`E=mgh.....................(2)`

Also, it should be recalled that the weight, W of an object is given by the equation below;

`W=mg...............(3)`

Substituting (3) into (2) we obtain the following;

`E=Wh..................(4)`

Given; h = 1.9m

To obtain the energy E converted by the lifter's body in Joules, we use the specifications given in the problem as follows;

Given; 1cal = 4186J

therefore 113cal = (113 x 4186)J = 473018J. This is the total energy contained in one ounce of cereal consumed by the lifter. However as specified by the problem, only 1.79% of this energy was converted by the lifter's body into weight lifting, therefore;

`E=(1.79)/(100)*473018J=8467.02J`

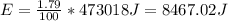
Putting this value of E into equation (4), we obtain the following;

`8467.02=W*1.9\\`

therefore;

`W=(8467.02)/(1.9)=4456.33N`

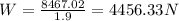
This is the heaviest weight of barbell the lifter could lift with the amount of energy specified.