Answer:
So the answer is DNC(Does Not Convergence)
Explanation:
Given;
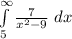
We know,
The integral is an improper integral because the upper limit of integration approaches infinity. First, replace the infinite upper limit by the finite limit 'l' and take the limit of 'l' to approach infinity.
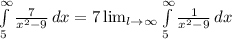
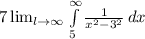
![7* \lim_(l \to \infty) \left [ (1)/(2* 3) \log\left |(x-3)/(x+3) \right | \right ]_(5)^(l)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/7quposru0ajhqxkipyno0gp6ful9nfr8qw.png) (∵We know;
(∵We know;
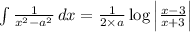 )
)
![(7)/(6) * \lim_(l \to \infty) \left[ \log\left | (l-3)/(l+3) \right |-\log\left | (5-3)/(5+3)\right |\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/rht13rap22fr8op3lzzoceyb2g5e9juaju.png)
![(7)/(6) * \lim_(l \to \infty) \left[ \log\left | (l-3)/(l+3) \right |-\log\left | (-2)/(8)\right |\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/w6oqenjvgu7j2ff1yi0y9ka0h22vpuo67b.png)
![(7)/(6) * \left[ \log\left | (\infty-3)/(\infty+3) \right |-\log( (2)/(8))\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/q8bzj64hk40e6dos5g6t2elffvdn6va2ny.png) (∵
(∵
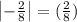 )
)
![(7)/(6) * \left[ \infty-\log( (2)/(8))\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/lxqi0l180es0rz4k40y2wk9xlkw015sr25.png)
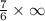
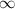
Thus the integral Does Not Convergence.