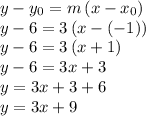Question

write the equation of the line with slope 3 that passes through the point (-1,6) in slope-intercept form

Answer 1

`y=3x+9`

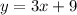
Explanation:

By knowing the slope of the line, and one point it has to go through, we can easily write the equation of the line by starting with the general form of a line in "point-slope" form. That is a line of slope "m" and going through the point
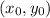`(x_0,y_0)` on the plane, can be written in its "point-slope" form as:

`y-y_0=m(x-x_0)` and subsequently solving for "y" in the equation to get it in its "slope-intercept" form.

Therefore, in our case, with slope (m) equal to 3, and the point
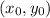`(x_0,y_0)` equal to (-1, 6), we get:

`y-y_0=m\,(x-x_0)\\y-6=3\,(x-(-1))\\y-6=3\,(x+1)\\y-6=3x+3\\y=3x+3+6\\y=3x+9`