Answer:
^(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/1848u2w237m7fkp27o8h43l5juh67pzzlv.png)
Explanation:
If -4 + 5i is a root of a polynomial, then it's conjugate -4 - 5i will also be a root of the same polynomial.
Therefore, the polynomial has 4 degree, and zeroes are (- 4 + 5i), (- 4 - 5i) and -1 with multiplicity 2.
Hence, the polynomial will be
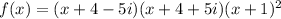
⇒
![f(x) = [x^(2) + 8x + (4 - 5i)(4 + 5i)] (x + 1)^(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/7f9umtvd7arohhrqcvhxl0253z7uh0b48p.png)
⇒
^(2)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/1848u2w237m7fkp27o8h43l5juh67pzzlv.png) (Answer)
(Answer)