Answer:
She did not multiply equation 3 in step 2 by the correct value.
Explanation:
Given:
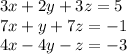
In order to solve this, we need to eliminate any one variable and then form a simultaneous equation with the remaining two variables. Then, we nee to solve the simultaneous equation.
Here, Galena is trying to eliminate the variable
 first.
first.
Step 1: She multiplies equation (3) by 3 and adds it to equation (1)
Let us multiply equation (3) by 3
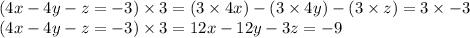
Now, adding this to equation 1 will cancel out z terms.

Now, she need to make one more equation in
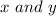 .
.
Step 2: She multiplies equation (3) by -7 and adds it to equation (2)
Multiplying equation (3) by -7 will give,

Now, adding this to equation 2 will not cancel out z terms.
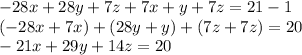
So, she makes mistake in step 2 as the
 terms are not being cancelled.
terms are not being cancelled.