Question

Suppose that the water level of a river is 34 feet and that it is receding at a rate of 0.5 foot per day. Write an equation for the water level, L, after d, days.

Answer 1

The equation to represent the rate of receding water level is L = 34
`(0.5)^(d)` .

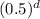Explanation:

Given as :

The initial level of water in river = 34 feet

The rate of receding water level = 0.5 foot per day

Or, The rate of percentage of receding water level = 50 % per day

Let the level of water after d days = L

Now,

The level of water after d days = initial level of water × (
`(1-(\textrm Rate)/(100))^(Time)`

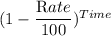
I.e L = 34 × (
`(1-(\textrm 50)/(100))^(d)`

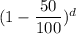
∴ L = 34 ×
`(0.5)^(d)`

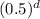
Hence The equation to represent the rate of receding water level is L = 34
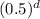`(0.5)^(d)` . Answer