Question

Suppose that the average number of accidents occurring on a highway each day is 3.5. Find the probability that at least two accidents occur today. Find the probability that at most one accident occurs today.

Answer 1

48 yards

Explanation:

Answer 2

Answer: 0.1359

Explanation:

This is a Poisson distribution. The formula for calculating Poisson distribution is given as :

P (X = x) =
`(e^(-λ)λ^(x))/(x!)`

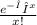
λ = 3.5

To find the probability that at most one accident occur today implies that , accident might not happen at all , the maximum accident that can happen is 1, substituting this into the formula , we have

P(X=0) =
`(e^(-3.5)3.5^(0) )/(0!)`

P(X=0) = 0.0302

P(X=1) =
`(e^(-3.5)3.5^(1) )/(1!)`

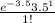
P(X=1) = 0.1057

Therefore , the probability that at most one accident occurs today.

= 0.0302 + 0.1057

= 0.1359

P(x=2) =
`(e^(-3.5)3.5^(2) )/(2!)`

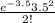
P(X=2) = 0.1850