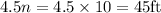Question

A rectangle swimming pool is 8 feet deep. One side of the pool is 4.5 times longer than the other. The amount of water needed for the swimming pool is 3600 ft.³ Find the dimensions of the pool.

Answer 1

The side lengths of the pool 10 ft and 45 ft.

SOLUTION:

Given, a rectangle swimming pool is 8 feet deep.

One side of the pool is 4.5 times longer than the other.

Let the length of pool be n feet, the width will be 4.5n feet

The amount of water needed for the swimming pool is 3600 cubic ft

We have to find the dimensions of the pool. Now, we know that,

`\begin{array}{l}{\text {volume of pool}=\text {depth} * \text {length } * \text {width}} \\\\ {\rightarrow 3600 \text { cubic } f t=8 \text { feet } * \text { n feet } *(4.5 n) \text { feet }} \\\\ {\rightarrow 8 n * 4.5 n=3600} \\\\ {\rightarrow 36 n^(2)=3600} \\\\ {\rightarrow n^(2)=100}\end{array}`

On taking square root on both sides we get,

`\begin{array}{l}{\rightarrow\sqrt{n^(2)}=√(100)} \\\\ {\rightarrow n=10 \mathrm{ft}}\end{array}`

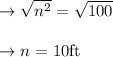
So, the width will be
`4.5 n=4.5 * 10=45 \mathrm{ft}`