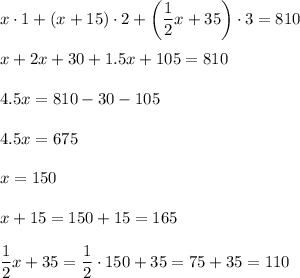Answer:
150 one point throws, 165 two points throws and 110 three points throws
Explanation:
Let x be the number of free (one point) throws.
The number of free throws Sarah made was 15 less than the number of two-point field goals she made. If y is the number of two points throws, then

so the number of two points throws
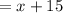
The number of two-point field goals that Sarah made was 55 less than double the number of three-point field goals she made. If z is the number of three points throws, then
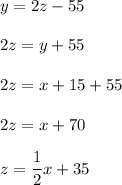
so the number of three points throws
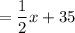
The total score is 810 points, so