Answer : The correct option is, The initial velocity is -44
Step-by-step explanation :
As we are given the position function expression:
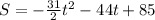
As we know that, differentiation of position function with respect to 't' gives velocity function.
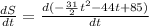
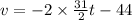
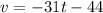
At time t = 0, the initial velocity will be:
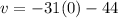
v = -44
Hence, the correct option is, The initial velocity is -44