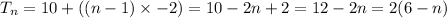Answer:
Expression in
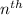 term is
term is
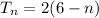
Explanation:
Arithmetic sequence 10,8,6,4,.....
first term a = 10
second term = 8
number of terms = n
common difference d = Second term - First term =
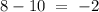
Now by using Arithmetic Progression Formula which states
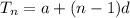
Substituting given values in the above expression we get