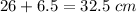Answer:
AE = 26 cm and AG = 32.5 cm
Explanation:
Given
AB = 12 cm
BD = 12 cm
FD = 6 cm
AC = 12 cm
AD = AB + BD =
Also segment BC is parallel segment ED which is parallel to segment GF
Now by midpoint theorem we can say that
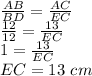
Now AE = AC + EC =
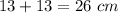
Also
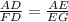
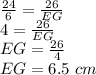
Now AG = AE + EG =