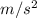Question

PLLLLLLLLLZ HELP 30 POINTS ANSWER ONLY IF YOU KNOW

A 50.0 kg wooden box is pushed across a floor with a constant speed of 2.5 m/s. The coefficient of kinetic friction is 0.20. If the force being applied to the box is tripled, what is the resulting acceleration on the box?

0.98 m/s2

0.784 m/s2

3.92 m/s2

196 m/s2

Answer 1

The resulting acceleration of the box is 3.92
`m/s^2`

Step-by-step explanation:

Please refer to the Free Body Diagram

According to the second Newton's Law, the acceleration of the mass will depend on the net force applied to it.

In the y-axis, the net force is zero since the mass won't move in that direction. We only need to analyze the dynamics on the x-axis.

The problem states that initially, the box moves at a constant speed which means zero acceleration, or zero net force.

If we analyze the forces on the x-axis we find:

F - Fr = m.a

Where F is the originally applied force, Fr is the Friction force, m is the mass of the box and a is the initial acceleration, which we found to be zero. Thus:

F - Fr = 0 => F = Fr =
`\mu`.N, being N the Normal force and
`\mu` the kinetic friction coefficient

By analyzing the y-axis, we find N = W = m.g

So N = 50 kg. 9.8
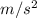`m/s^2` = 490 Nw

The Friction force is then:

Fr = 490 Nw . 0.2 = 98 Nw

Which gives us the initial Force:

F = 98 Nw

When tripled, the new Force will be

F' = 294 Nw

And the corresponding x-axis equilibrium condition is:

F' - Fr = m.a' ....(a' is the resulting acceleration). So we have:

`a=(F'-Fr)/(m)=(294Nw-98Nw)/(50 Kg)  =(196Nw)/(50Kg)`

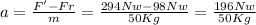
a = 3.92
`m/s^2`