Question

A square is cut out of a circle whose diameter is approximately 14 feet. What is the approximate area (shaded region) of the remaining portion of the circle in square feet? ( where A=rrx2 rr =3.14

Answer 1

Answer: 56 square feet

Explanation:

When a square is inscribed within a circle, the side length of the square is equal to the diameter of the circle, divided by the square root of 2, this is the same as a square being cut out of the circle.

This means that area of the square =
`((14)/(√(2) )) ^(2)`

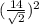
= 98 square feet

Area of the circle is
`\pi`
`r^(2)`

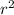
= 3.142 X 7 X 7

= 153.958

Area of the remaining portion will be Area of the circle - Area of the square , that is

153 . 958 - 98

= 55. 958

≈ 56 square feet