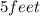Question

Can anyone please help me with this ?

Answer 1

Distance from point A to the top of the building(hypotenuse)=
`5√(2)feet`

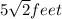
Height of the landscaper=
`5 feet`

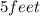
Explanation:

Given:

Distance from point A to bottom of building = 5 feet

Angle of depression from the top of building = 45°

We see that the triangle formed is a special 45-45-90 right triangle

The sides of such triangle is given by:

Leg1 =
`x`

Leg2=
`x`

Hypotenuse =
`x√(2)`

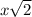
We know the
`x=5 feet`

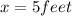
So we can find all the sides of the triangle:

Leg1 =
`5 feet`

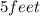
Leg 2 =
`5 feet`

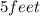
Hypotenuse=
`5√(2)feet`

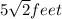
It is shown in figure attached.

Distance from point A to the top of the building(hypotenuse)=
`5√(2)feet`

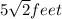
Height of the landscaper=
`5 feet`

Answer 2

The distance from point A to the top of the building is 5
`√(2)` feet

The Height of the Skyscraper is 5 feet

Explanation:

Given

Let Top point of building be point C

Also Let Base of the building be point B

Distance from point A to base B of the building AB= 5 feet

∴ It makes a Right angle triangle

Also ∠ACB = 45°

Also tan 45° = 1

Now tan ∠ACB =
`(AB)/(BC)`

∴ AB= BC =5 feet

The Height of the Skyscraper is 5 feet

Now Triangle ABC is right angle triangle with right angled at B

So by Pythagoras theorem

AC=
`√(AB^2+BC^2)=√(5^2+5^2) =√(50) =√(25*2) =√(5^2*2)=5√(2)`

The distance from point A to the top of the building is 5
`√(2)` feet