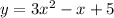Question

Find the equation of the parabola that passes through the points:
(0,5) (1,7) and (-2,19)

Answer 1

The equation of the parabola is:
`y=3x^2-x+5`

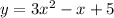
Explanation:

The standard form of a parabola is given as:

`y=ax^2+bx+c`

The three points on the parabola are (0,5), (1,7), and (-2,19).

Plug in the three points and find three equations in a,b and c

Using point (0,5) in the equation, we get

`a(0)^2+b(0)+c=5\\c=5`

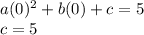
Using point (1,7) in the equation, we get

`a(1)^2+b(1)+c=7\\a+b+c=7`

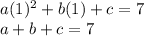
Using point (-2,19) in the equation, we get

`a(-2)^2+b(-2)+c=19\\4a-2b+c=19`

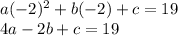
Plug in the value of c=5 in the last two equations. This gives,

`a+b+5=7\\a+b=7-5\\a+b=2----- 4\\\\4a-2b+5=19\\4a-2b=19-5\\4a-2b=14\\2(2a-b)=14\\2a-b=7`

Now, add the two new equations. This gives,

`a+b+2a-b=2+7\\ 3a=9\\a=(9)/(3)=3`

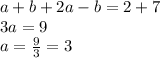
Now, plug in
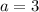`a=3` in equation 4 gives,

`3+b=2\\b=2-3=-1`

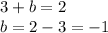
Therefore, the equation of the parabola is:

`y=3x^2-x+5`