Question

The length of a rectangle is (2x –1) units, and the width is (x − 2) units. The area of the rectangle is 20 square units. What is the length of the rectangle?

A. 0.5 units

B. 3 units

C. 4.5 units

D. 8 units

Answer 1

Length of the given rectangle is 8 units.

Option - D

Solution:

Given that

Length of a rectangle =
`(2x-1)\text { units}`

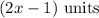
Width of a rectangle =
`(x-2)\text{ units}`

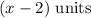
Area of rectangle = 20 square units

Need to calculate length of rectangle.

`\text { Formula of area of rectangle }=\text { Length of a rectangle } * \text { Width of a rectangle }`

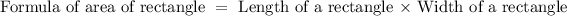
Substituting given value of Area of rectangle and expressions for length and width of rectangle in formula, we get

`20=(x-2)(2 x-1)`

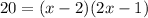
On solving above equation for x we get

`\begin{array}{l}{20=x(2 x-1)-2(2 x-1)} \\\\ {\Rightarrow 20=2 x^(2)-x-4 x+2} \\\\ {\Rightarrow 2 x^(2)-5 x+2-20=0} \\\\ {\Rightarrow 2 x^(2)-5 x-18=0}\end{array}`

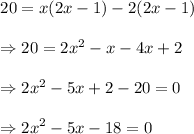
On splitting the middle term in such a way that product of split terms comes as
`2x^2* -18 = -36x^2` and summation comes as -5x, we get

`\begin{array}{l}{\Rightarrow 2 x^(2)+4 x-9 x-18=0} \\\\ {=>2 x(x+2)-9(x+2)=0} \\\\ {\Rightarrow(2 x-9)(x+2)=0} \\\\ {\Rightarrow(2 x-9)=0 \text { or }(x+2)=0} \\\\ {\Rightarrow x=(9)/(2) \text { or } x=-2}\end{array}`

`\begin{array}{l}{\text { When } x=(9)/(2), \text { length }=(2 x-1) \text { units }=\left(2 * (9)/(2)-1\right)=8 \text { units }} \\\\ {\text { When } x=-2, \text { length }=(2 x-1) \text { units }=(2 *(-2)-1)=-5 \text { units }}\end{array}`

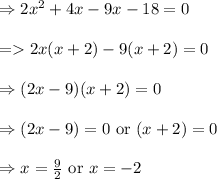
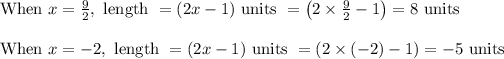
As length cannot be negative hence we can ignore negative value.

So length is 8 units.