Question

A conducting rod (length = 2.0 m) spins at a constant rate of 2.0 revolutions per second about an axis that is perpendicular to the rod and through its center. A uniform magnetic field (magnitude = 8.0 mT) is directed perpendicularly to the plane of rotation. What is the magnitude of the potential difference between the center of the rod and either of its ends?

Answer 1

0.050V

Step-by-step explanation:

To solve this problem it is necessary to use the concepts related to the potential between two objects that have a magnetic field, this concept is represented in the equation.

`\int dV = \int_(0)^(l/2) Bv (dl)`

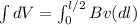
Where,

v= tangencial velocity

B = Magnetic Field

We know for definition that,

`v= l\omega`

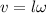
Where,

L = length

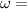`\omega =` Angular velocity

We can replace this values in our first equation then,

`\int dV = \int_(0)^(l/2) B (l\omega) (dl)`

Integrating we have,

`V = (1)/(8) Bl^2 \omega`

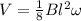
Replacing the values,

`V= (1)/(8) (8*10^(-3))(12.56)(4)`

`V = 0.050V`

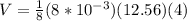
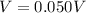
Therefore the potential difference between the center of the rod and the other rod is 0.050V