Question

Suppose that a ball is dropped from a building that is 96 ft high. After t seconds, the height of the ball is f(t) = 96 − 16t 2 ft. 1. What is the instantaneous velocity of the ball t = 2 seconds after it is dropped? 2. How fast is the ball traveling when it hits the ground?

Answer 1

1) v(t=2s) = - 64 ft/s

2) vf= 78.4 ft/s

Step-by-step explanation:

height of the ball as a function of time

h= f(t) = 96 − 16t² ft Equation (1)

Instantaneous velocity of the ball t = 2 seconds after it is dropped

v=dh/dt=-32 t Equation (2): Instantaneous velocity

v(t=2s)= -32*2 = -64 ft/s

Speed of the ball when it hits the ground

When the ball hits the ground , h=0 , then, We replace data in the equation (1) to calculate the time it takes for the ball to touch the ground

h = 96 − 16t²

0 = 96 − 16t²

16t² = 96

t² = 96 /16 =6

`t= (√(6) ) s`

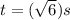
t = 2,45 s

We apply the kinematic equation of the ball in free fall

vf= v₀+gt Formula (1)

Where:

t : time in seconds (s)

v₀: initial speed in ft/s

vf: final speed in ft/s

g: acceleration due to gravity in ft/s²

Data

v₀= 0

t = 2,45 s

g = 32 ft/s²

We replace data in the formula (1)

vf= v₀+gt

vf= 0+ (32)(2,45)

vf= 78.4 ft/s