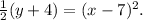Question

1/2 (y+4)=(x-7)^2 in vertex form step by step

Answer 1

`y=2(x-7)^(2)-4` is vertex form of equation
`(1)/(2)(y+4)=(x-7)^(2)`

Solution:

Need to determine vertex form of the following equation

`(1)/(2)(y+4)=(x-7)^(2)`

Generic Vertex form of a quadratic equitation is as follows

`\mathrm{y}=\mathrm{a}(x-\mathrm{h})_(n)^(2)+\mathrm{k} \quad \text { where }(\mathrm{h}, \mathrm{k}) \text { are vertex }`

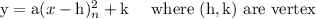
So what we have to do is first make coefficient of y = 1 in our equation.

`y+4=2(x-7)^(2)`

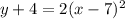
Now on Left hand side keep only y and move all the remaining term to right hand side

`\Rightarrow y=2 (x-7)^2-4\Rightarrow(1)`

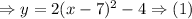
On comparing equation (1) with generic vertex form equation we can say that In our case a = 2, h = 7 and k = -4

Hence
`y=2(x-7)^(2)-4` is vertex form of equation
`(1)/(2)(y+4)=(x-7)^(2).`