Answer:
42.4m/s
Step-by-step explanation:
To develop the problem it is necessary to apply the concepts related to thermodynamic work and Bernoulli's principle in which the behavior is described of a liquid moving along a stream.
The work of an incomprehensible liquid is given by the equation,
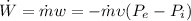
Where,
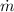 = Mass flow
= Mass flow
 = Specific Volumen
= Specific Volumen
P = Pressure
Our values are given by,
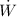 = 2kW
= 2kW
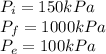
 Table 1 for saturated water in 10°C
Table 1 for saturated water in 10°C
We need to find the mass flow, then re-arrange for
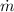
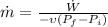
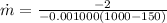
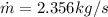
To find the Spray velocity, we apply Bernoulli equation, because at the Nozzle there is not Work or Heat transfer related. Then,
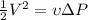

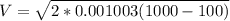
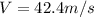
Therefore the spray velocity is 42.4m/s