Question

LetFbe the the vector space of all real functions. (The functions are "vectors" inF).a) (2 points) Is the set of functions of the formf(x) =ax4+bx2+c, wherea,b,ccan be any real numbers,a subspace ofF? If not, explain why.b) (2 points) Is the set of functions of the formf(x) =ax2+bx+ 1, whereaandbcan be any real numbers,a subspace ofF? If not, explain why.c) (4 points) Find the basis for the function subspace containing the following functionsa+b+c= 0; 2a−b=c.

Answer 1

a) Yes, it is

b) No, it isnt

c) < sen(x) - cos (x) >

Explanation:

A subset S from a R-vector space V is a subspace is:

• For each s ∈ S, v ∈ R, then v*s ∈ S

• For each pair s1, s2 ∈ S, s1+s2 ∈ S

a) Lets call A the set of all real valued functions of the form
`ax^4 + bx^2 + c` .

Given f ∈ A,
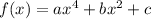`f(x) = ax^4 + bx^2 + c` , for certain real numbers a,b,c , and given r ∈ R. We have that
`r*f = r * (ax^4 + bx^2 + c)  = ra*x^4 + rb x^2 + rc`

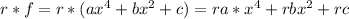
Since ra, rb and rc are real numbers, then r*f ∈ A.

Now lets suppose f1 are f2 are functions in A, with
`f_1(x) = a1x^4 + b1x^2 + c1` ,
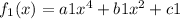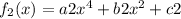`f_2(x) = a2x^4 + b2x^2 + c2` . Then

`f_1(x) + f_2(x) = a1x^4 + b1x^2 + c1 + a2x^4 + b2x^2 + c2 = (a1+a2) x^4 + (b1+b2) x^2 + (c1+c2)`

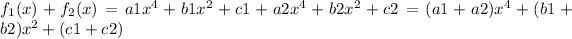
Since a1+a2 , b1 +b2 and c1+c2 are all real numbers, then f1+f2 is an element of A.

Therefore A is a vector subspace of F.

b) Lets call B the subset of funtions of the form f(x) =ax²+bx+ 1. You can note that every single function of B have a 1, that means, each function f satisfies f(0) = 1. We can easily exploit this property to reach the conclussion that B is not a vector subspace of F.

For example, we can consider the function f(x) = x² + x + 1. Clearly f is an element of B because it satisfies the conditions. However if we multiply by the real number 2 we obtain that 2*f (x) = 2x² + 2x + 2, which is not an element of B because it doesnt have 1 as independent term. Therefore B is not a linear subspace.

c) Lets analyze what possible values a,b and c may have. Since a+b+c = 0, then c = -b-a. Replacing this value of c on the other equation we have that

2a-b = -b-a, or equivalently 3*a = 0

Thus, a = 0, and by replacing this value on the first equation we have that c = -b. As a result, (a,b,c) = (0,b,-b) = b * (0, 1, -1). Therefore, the combination (a,b,c) must be a real multiple of (0,1,-1). Replacing by that value, we have that a basis for the subspace is < sen(x) - cos (x) >

I hope this helped you!