Question

Some more questions

Answer 1

1. D

2. D

3. B

4. C

Explanation:

1.

The distributive property is shown below:

`a(b+c)=ab+ac`

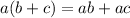
This means we have to multiply the outside number (a) with both the inside numbers (b & c). For example, if we had the expression:

3(4+2)

We would multiply "3" with both 4 and 2 and take their sum. Shown below:

3*4 + 3* 2

Now, to our quesstion. it tells us to use distributive property on the expression:

4(3+7)

So we have to multiply "4" with both 3 and 7 and take the sum. Shown below:

4*3 + 4*7

Correct answer choice is D

2.

We can use algebraic manipulations on this expression to make it into another exxpression which is equal to this, so putting any value of "x" won't make a difference.

We can use the distributive property, so simplify this expression. Shown below:

`a(b+c)=ab+ac`

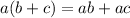
This means we have to multiply whatever's outside with 2 inside expression and take their sum.

We have to simplify
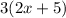`3(2x+5)`. So we have to multiply "3" with "2x" and "5" individually and take the sum. That would be:

`3(2x+5)\\=3(2x) + 3(5)\\=6x + 15`

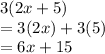
Correct choice is D

3.

The distributive property is given below:

`a(b+c)=ab+ac`

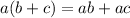
This tells us that if their is a sum inside parenthesis multiplied by another number in front, we have to individually multiply each number inside parenthesis with whatever's outside.

Looking at the choices, we can eliminate A first, since it's just addition.

C is eliminated because it shows multiplication.

D is also eliminated because it just turns around the problem.

B is correct choice because it shows "11" the outside number, multiplied individually with the 2 inner numbers, "5" and "2", respectively.

B is correct.

4.

We have to take out the GCF of 12 and 90 as common. First, lets get the GCF of these 2 numbers.

We list out the factors of both 12 and 90 and see the greatest of them all that is common.

The factors of 12 are 1,2,3,4,6,12

The factors of 90 are 1,2,3,5,6,9,10,15,18,30,45,90

Out of the common factors, 6 is the largest. So GCF(12,90) = 6

We have to take "6" as common. That immediately tells us that C is the correct choice.

If we take out 6, we have:

12 + 90

= 6(2 + 15)

C is right choice.