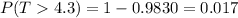Question

A plastic casing for a magnetic disk is composed of two halves. The thickness of each half is normally distributed with a mean of 2 millimeters (mm) and a standard deviation of 0.1 mm, and the halves are independent. Determine the mean and s.d. the total thickness of the two halves. What is the probability that the total thickness exceeds 4.3 mm?

Answer 1

The mean is 4 mm and the standard deviation is 0.1414 mm

`P(T>4.3)=0.017`

Explanation:

Let's start defining the random variables.

`T_(1)` : ''Thickness in mm of the first half''

`T_(2)` : ''Thickness in mm of the second half''

The mean for this random variables is 2 (mm)

The standard deviation for this random variables is 0.1 mm

`T_(1)` ~ N(2,0.1)

`T_(2)` ~ N(2,0.1)

Now we calculate the variance of each random variable.

`(StandardDeviation)^(2)=Variance`

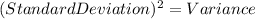
Therefore,

`(0.1mm)^(2)=0.01(mm^(2))`

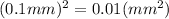
The total thickness ''T'' is equal to

`T=T_(1)+T_(2)`

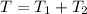
Because of the independence between the halves and that T is the sum between two normally distributed random variables,

T ~ N [μ1 + μ2,
`√(Var(T1)+Var(T2))`]

Where μ is the mean of the random variable

Where the mean for T is the sum of the means between
`T_(1)` and
`T_(2)` and the variance of T is the sum between the variances of
`T_(1)` and
`T_(2)`

μ1 + μ2 = 2 + 2 = 4

Var(T1) + Var(T2) = 0.01 + 0.01 = 0.02

The mean for T is 4 mm and the variance is
`0.02(mm^(2))`

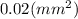
The standard deviation is

`√(0.02)=0.1414`

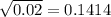
The standard deviation is 0.1414 mm

T ~ N (4,0.1414)

`P(T>4.3)=1-P(T\leq 4.3)`

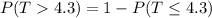
We subtract the mean and then we divide all by the standard deviation to obtained N(0,1)

Z ~ N(0,1) ⇒

`1-P(T\leq 4.3)=1-P((T-4)/(0.1414)\leq(4.3-4)/(0.1414))`

`P(T>4.3)=1-P(Z\leq 2.1216)=` 1 - φ(2.1216)

Where φ(2.1216) is the value of the cumulative distribution of N(0,1) evaluated in 2.1216 (You can find this value on a table)

`P(T>4.3)=1-0.9830=0.017`