Question

Can I please have help, I don't know how to solve this.

3741 = P(P-1) over 2

Answer 1

The values of P are -87 or 86.

Explanation:

Given:

`3741=(P(P-1))/(2)`

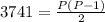
Multiply by 2 on both the sides. This gives,

`3741* 2=(P(P-1))/(2)* 2\\7482=P(P-1)`

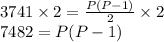
Now, use distribution property.

`7482=P* P - P* 1\7482=P^2-P`

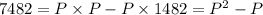
Now, add -7482 on both sides,

`P^2-P-7482=0`

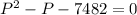
This is a quadratic equation of the form
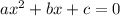`ax^2+bx+c=0` which can be solved using quadratic formula with
`a=1,b=-1,c=-7482`

`P=(-b\pm √(b^2-4ac))/(2a)\\P=(-1\pm√((-1)^2-4(1)(-7482)))/(2(1))\\P=(-1\pm√(1+29928))/(2)\\P=(-1\pm√(29929))/(2)\\P=(-1-173)/(2)\textrm{ or }P=(-1+173)/(2)\\P=(-174)/(2)\textrm{ or }P=(172)/(2)\\P=-87\textrm{ or }P=86`

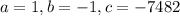
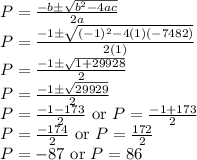
Therefore, the values of P are -87 or 86