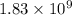Answer : The conditional formation constant is
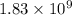
Explanation :
First we have to calculate the formation constant.
As we are given that:
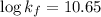
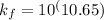
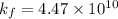
Thus, the formation constant is
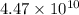
Now we have to calculate the conditional formation constant.
The expression used as:
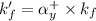
where,
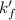 = conditional formation constant = ?
= conditional formation constant = ?
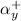 = activity coefficient at pH 9.00 = 0.041
= activity coefficient at pH 9.00 = 0.041
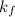 = formation constant =
= formation constant =
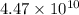
Now put all the given values in the above expression, we get:
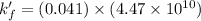
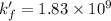
Therefore, the conditional formation constant is