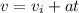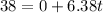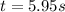Answer:
Step-by-step explanation:
As we know that the coefficient of static friction between box and the truck is given as
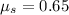
so the maximum static friction force on the box so that it will not slide on the truck is given as

so maximum possible acceleration of the box is given as
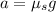

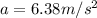
now time to reach the given speed is