Question

Because of variability in the manufacturing process, the actual yielding point of a sample of mild steel subjected to increasing stress will usually differ from the theoretical yielding point. Let p denote the true proportion of samples that yield before their theoretical yielding point. If on the basis of a sample it can be concluded that more than 20% of all specimens yield before the theoretical point, the production process will have to be modified.

(a) If 9 of 40 specimens yield before the theoretical point, what is the P-value when the appropriate test is used? (Round your answer to four decimal places.) P-value

Answer 1

P-value ≈ 0.3463

Explanation:

Hypothesis test would be

`H_(0)`:p=0.20

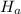`H_(a)`:p>0.20

We need to calculate the z-score of sample proportion and then the corresponding P-value.

z-score can be calculated as:

z=
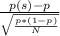`\frac{p(s)-p}{\sqrt{(p*(1-p))/(N) } }` where

• p(s) is the sample proportion of specimens yield before the theoretical point (
  `(9)/(40)=0.225`)

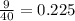• p is the proportion assumed under null hypothesis. (0.20)

• N is the sample size (40)

Using the numbers

z=
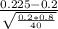`\frac{0.225-0.2}{\sqrt{(0.2*0.8)/(40) } }` =0.3953

and the P-value is then P(z)≈0.3463