Question

Billiard ball A of mass mA = 0.117 kg moving with speed vA = 2.80 m/s strikes ball B, initially at rest, of mass mB = 0.141 kg . As a result of the collision, ball A is deflected off at an angle of θ′A = 30.0∘ with a speed v′A = 2.10 m/s, and ball B moves with a speed v′B at an angle of θ′B to original direction of motion of ball A.

Answer 1

vB' = 1.19 m/s

θB' = 47°

Step-by-step explanation:

mA = 0.117 kg

vA = 2.80 m/s

mB = 0.141 kg

vB = 0

vA' = 2.10 m/s at an angle θA' = 30°

vB' = ?,

Let the ball B makes an angle θB' below X axis as shown.

Use conservation of momentum along X axis

mA x vA + mB x 0 = mA' x vA' CosθA' + mB' x vB' CosθB'

0.117 x 2.80 = 0.117 x 2.10 x Cos30 + 0.141 x vB' CosθB'

0.3276 = 0.213 + 0.141 x vB' CosθB'

vB' CosθB' = 0.813 .... (1)

Use conservation of momentum along Y axis

mA x 0 + mB x 0 = mA' x vA' SinθA' - mB' x vB' SinθB'

0 = 0.117 x 2.10 x Sin30 + 0.141 x vB' SinθB'

vB' SinθB' = - 0.871 .... (2)

Squarring and adding both the equations

`v_(B)'\left ( Cos^(2)\theta _(B)'+Sin^(2)\theta _(B)' \right )=\left ( -0.871 \right )^2+0.813^(2)`

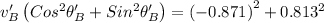
vB' = 1.19 m/s

Divide equation (2) by equation (1), we get

tanθB' = - 1.07

θB' = 47°

Thus, the speed of ball B after collision is 1.19 m/s and it makes an angle 47° from X axis downward.

Answer 2

Step-by-step explanation:

Let the velocity of ball B after collision be v′B at angle θ′B with original direction.

We shall apply law of conservation of momentum in the direction perpendicular to the direction of motion before collision.

Initial momentum before collision in that direction = 0

Final momentum after collision in that direction

= 2.1 x .117 sin 30 - v sinθ′B

so

2.1 x .117 sin 30 - v sinθ′B= 0

v sinθ′B = .122

Initial momentum before collision in the direction of original motion = final momentum after collision in the direction of original motion

2.1 x .117 cos 30 - v cosθ′B = .117 x 2.8 +0

v cosθ′B = .1156

v²( sin²θ′B + v cos²θ′B )² = .1156² + .122²

v = .168

v cosθ′B = .1156

.168 cosθ′B = .1156

cosθ′B = .1156 / .168

θ′B = 46.5 degree.