Question

Determine the equation of the tangent line to the given path at the specified value of t. (Enter your answer as a comma-separated list of equations in (x, y, z) coordinates.) (sin(5t), cos(5t), 2t7/2); t = 1

Answer 1

(Sin(5)+5Cos(5), Cos(5)-5Sin(5), 9)

Explanation:

The equation of tangent line is
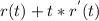`r(t)+t*r^(')(t)`, then:

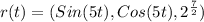`r(t)=(Sin(5t), Cos(5t), 2^{(7)/(2) } )` and
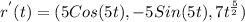`r^(') (t)=(5Cos(5t), -5Sin(5t), 7t^{(5)/(2) })`, we have to (x,y,z) coordinates

x=r(t)+tr'(t), y=r(t)+tr'(t), z=r(t)+tr'(t); so x=Sin(5t)+t(5Cos(5t)), y=Cos(5t)+t(-5Sin(5t)),
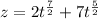`z=2t^{(7)/(2) }+7t^{(5)/(2) }`, to t=1 then:

x=Sin(5)+5Cos(5), y=Cos(5)-5Sin(5), Z=9; Finally (Sin(5)+5Cos(5), Cos(5)-5Sin(5), 9)