Question

Find the slope of the line running
through these two points (-4,5) and (8,-3)

Answer 1

The slope the line that passes through the given points is
`\bold{(-3)/(4)}`

SOLUTION:

Given, two points are (- 4, 5) and (8, -3). We have to find the slope of a line that passes through the above given two points.

We know that, slope of a line that pass through
`\bold{(x_1, y_1) \text{ and } (x_2, y_2) \text{ is given by } \mathrm{m}=(y_(2)-y_(1))/(x_(2)-x_(1))}`

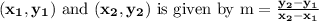
Here, in our problem,
`x_(1)=-4; y_(1)=5 \text { and } x_(2)=8; y_(2)=-3`

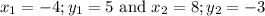
Now, slope
`\bold{m=(-3-5)/(8-(-4))=(-8)/(8+4)=(-8)/(12)=(-3)/(4)}`

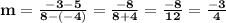
Hence, the slope is
`(-3)/(4)`

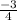
The following are the steps in calculating the slope of a straight line:

• Step One: Identify two points on the line.

• Step Two: Select one to be
  `(x_1, y_1)` and the other to be
  `(x_2, y_2)`

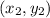
• Step Three: Use the slope equation to calculate slope.

Answer 2

The slope is

`(-3-5)/(8-(-4)) =(-8)/(8+4) =(-8)/(12) =-(2)/(3)`

Explanation: