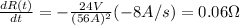Answer:
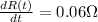
Step-by-step explanation:
Since
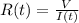 , we calculate the resistance rate by deriving this formula with respect to time:
, we calculate the resistance rate by deriving this formula with respect to time:
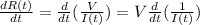
Deriving what is left (remember that
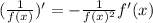 ):
):
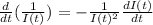
So we have:
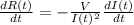
Which for our values is (the rate of I(t) is decreasing so we put a negative sign):