Question

Determine the projection (magnitude and sign), or component, of vector v1 along the direction of vector v2. Your answer could be positive or negative, or zero, make sure you indicate the correct sign. Draw the vectors and see if your answer makes sense! v1=( -5, 7 , 2) ft v2=(3, 1, 2) ft

Answer 1

- 1.07 ft

Step-by-step explanation:

V1 = (-5, 7, 2)

V2 = (3, 1, 2)

Projection of v1 along v2, we use the following formula

=\frac{\overrightarrow{V1}.\overrightarrow{V2}}{V2}

So, the dot product of V1 and V2 is = - 5 (3) + 7 (1) + 2 (2) = -15 + 7 + 4 = -4

The magnitude of vector V2 is given by

=
`\sqrt{3^(2)+1^(2)+2^(2)}=3.74`

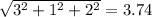
So, the projection of V1 along V2 = - 4 / 3.74 = - 1.07 ft

Thus, the projection of V1 along V2 is - 1.07 ft.

so we need to find the direction of v2