Answer:
Horizontal stretch by a factor of 3
Explanation:
Given:
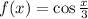

Function transformation rule used:
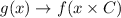
When
 is multiplied by a constant
is multiplied by a constant
 then the function is either stretched or compressed in horizontal direction.
then the function is either stretched or compressed in horizontal direction.
If the
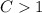 then its a horizontal compress.
then its a horizontal compress.
If the
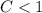 then its a horizontal stretch.
then its a horizontal stretch.
Function transformation taking place:
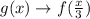
The constant term multiplied in the above transformation comes to be
 which is
which is
 , which means that the transformation would be a horizontal stretch by a factor of 3.
, which means that the transformation would be a horizontal stretch by a factor of 3.