Question

What is the axis of symmetry of the equation?

y = (x - 3)^2 + 4

x = -3
x = 3
x = -4
x = 4

Answer 1

x = 3

Explanation:

Every quadratic is symmetrical about the line: x = h, where h is the x-coordinate of the vertex

Answer 2

x = 3

Explanation:

The standard form of a parabola (x^2 function) is:

`y=ax^2+bx+c`

If we algebraically manipulate this, we can have the vertex form:

`y=a(x-h)^2 + k`

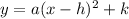
Where

x = h will be the axis of symmetry

k will be the vertical shift

(h,k) would be the vertex

Now, the function given in this problem is given in vertex form:

`y=(x-3)^2 + 4`

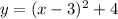
From the original vertex form, we can say that this equation has the folllowing variable values:

a = 1

(3,4) is the vertex

x = 3 is the axis of symmetry

4 is the vertical shift

We are concerned with axis of symmetry. Thus, we can see that

x = 3 is the axis of symmetry