1 Answer

Carmen · Answer 1 · 2020-10-02T21:46:41+0000

For this case we must find the solution of the following inequalities:

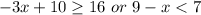
$-3x + 10 \geq16\ or\ 9-x <7$

So:

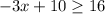
$-3x + 10 \geq16$

Subtracting 10 from both sides of the inequality:

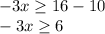
$-3x \geq16-10\\-3x \geq6$

Dividing by 3 to both sides of the inequality:

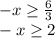
$-x \geq \frac {6} {3}\\-x \geq2$

We multiply by -1 on both sides taking into account that the sense of inequality changes:

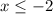
$x \leq-2$

Thus, the solution is given by all values of x less than or equal to -2.

Also we have:

9-x <7

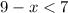
Subtracting 9 from both sides of the inequality:

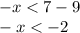
$-x <7-9\\-x <-2$

We multiply by -1 on both sides taking into account that the sense of inequality changes:

x> 2

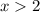
Thus, the solution is given by all values of x greater than 2.

Therefore, the solution set is given by:

(-∞, -2] U (2, ∞)

Answer:

(-∞, -2] U (2, ∞)

Please log in or register to add a comment.