Answer:
1.08m/s
Step-by-step explanation:
To develop this problem it is necessary to resort to the concept developed by Bernoulli in his equations in which
describes the behavior of a fluid along a channel.
Bernoulli's equation is given by

Where,
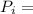 Pressure at determinated point
Pressure at determinated point
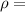 density (water in this case)
density (water in this case)
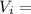 Velocity at determinated point
Velocity at determinated point
g = Gravity acceleration
z = Pressure heads at determinated point.
We know that the problem is given in an horizontal line, then the pressure heads is zero.
And for definition we know that,
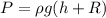
Where h means the heights of water column measured by the pitot tube at the top and the piezometer. Then replacing both pressure with the previous values we have:
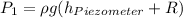

Then replacing
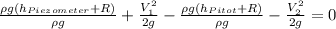

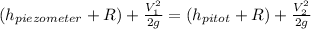
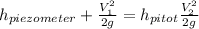
At the end of the pipe the speed is zero, since there is stagnation then:
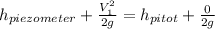

Re-arrange for
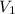 =
=
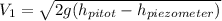
Replacing the values where
 and
and
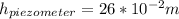 we have,
we have,
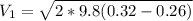
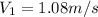
Therefore the velocity at the centerline is 1.08m/s