Question

Suppose that in a certain population, individuals’ heights are approximately nor-mally distributed with parametersμ=70 andσ=3 in.a.What proportion of the population is over 6 ft. tall?b.What is the distribution of heights if they are expressed in centimeters? Inmeters?

Answer 1

a) 25.14% of the population is over 6ft tall.

b) Both are going to be normally distributed.

Centimeters:
`\mu = 177.8, \sigma = 7.62`cm

Meters:
`\mu = 1.778, \sigma = 0.0762`cm

Explanation:

Problems of normally distributed samples can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

In this problem, we have that:

Normally distributed with parameters
`\mu = 70, \sigma = 3`.

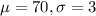a.What proportion of the population is over 6 ft. tall?

We have to convert from ft to inches.

Each feet has 12 inches, so 6ft = 72in.

This proportion is 1 subtracted by the pvalue of Z when
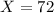`X = 72`. So

`Z = (X - \mu)/(\sigma)`

`Z = (72 - 70)/(3)`

`Z = 0.67`

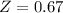
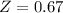`Z = 0.67` has a pvalue of 0.7486.

This means that 1-0.7486 = 0.2514 = 25.14% of the population is over 6ft tall.

b.What is the distribution of heights if they are expressed in centimeters? Inmeters?

It is going to still be normally distributed. We just have to convert the mean and the standard deviation from inches to centimeters and meters.

In centimeters.

Each inch has 2.54cm. So it is going to be normally distributed with
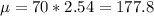`\mu = 70*2.54 = 177.8`cm and
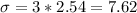`\sigma = 3*2.54 = 7.62`xm

In meters

Each m has 100cm. So

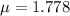`\mu = 1.778`m,
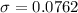`\sigma = 0.0762`m.