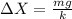Question

What is the net force at the equilibrium point? Derive an equation for the location of the equilibrium point based on the acceleration due to gravity, the hanging mass, the spring constant and the position of the mass when the spring is unstretched.

Answer 1

To find a general equilibrium point for a spring based on the hook law, it is possible to start from the following premise:

Hook's law is given by:

`F = k\Delta X`

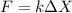
Where,

k= Spring Constant

`\Delta X =` Change in Length

F = Force

When there is a Mass we have two force acting at the System:

W= mg

Where W is the force product of the weigth. Then the force net can be defined as,

`F_(net) = F+W`

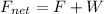
But we have a system in equilibrium, so

`0 = K\Delta X -mg`

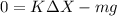
We find the equilibrium for any location when

`\Delta X = (mg)/(k)`