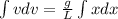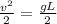Answer:
Part a)
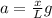
Part b)
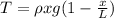
Part c)

Step-by-step explanation:
Part a)
Net pulling force on the chain is due to weight of the part of the chain which is over hanging
So we know that mass of overhanging part of chain is given as

now net pulling force on the chain is given as

now acceleration is given as

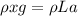
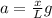
Part b)
Tension force in the part of the chain is given as
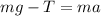
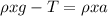
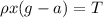

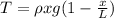
Part c)
velocity of the last link of the chain is given as
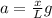

now integrate both sides