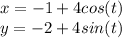Question

Find a parametrization of the circle of radius 4 in the xy-plane, centered at (−1,−2), oriented counterclockwise. The point (3,−2) should correspond to t=0. Use t as the parameter for all of your answers.

Answer 1

`x=-1+4cos(t),y=-2+4sin(t)`

Explanation:

To construct a parametric function, we can simply think that we are using vectors to draw.

1. Firstly, we define the center, which is (-1,-2). We can do this by constructing vector [-1,-2], which points exactly to the center of the circle
2. (Refers to the picture below) Recall from trigonometry that radius vector of a circle with radius R can be broken down into x and y vector component with magnitude R cos(t) and R sin(t) respectively, where t is angular distance. Thus, the vector that can be used to define circle with radius 4 is [4 cos(t),4 sin (t)]
3. By the linearity of the vector, we can superimpose 2 vectors obtained from above to get the result in which a circle with center at (-1,-2) and radius 4 is drawn.

By superimposing, we get vector [-1+4cos(t),-2+4sin(t)]

In parametric function term, this means that the coordinate (x,y) of this function is defined by

`x=-1+4cos(t)\\ y=-2+4sin(t)`