Answer: b) 6
Explanation:
Given : The illuminance of a surface varies inversely with the square of its distance from the light source.
i.e. for d distance and l luminance , we have
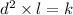 , where k is constant. (1)
, where k is constant. (1)
If the illuminance of a surface is 120 lumens per square meter when its distance from a certain light source is 6 meters.
From (1), we have
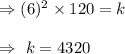 (2)
(2)
For the distance (d) corresponds to the illuminance to 30 lumens per square meter , we have
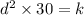
Put value of k , we get
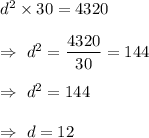
Then , the number of meters should the distance of the surface from the source be increased= 12 meters- 6 meters = 6 meters.