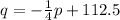Answer:
Explanation:
Given:
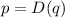 is a linear model for demand function
is a linear model for demand function
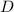
where
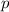 represents the price per item in dollars and
represents the price per item in dollars and
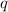 is the quantity demanded.
is the quantity demanded.
With increase in
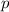 by $8 there is a decrease in
by $8 there is a decrease in
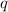 by 2 items.
by 2 items.
For
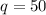 items purchased the price
items purchased the price
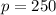 .
.
To find
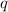 as a function of
as a function of
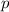 which is
which is
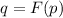
Since its a linear model, so we can find rate of change or slope of line from the given data.
Slope
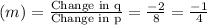
So, the function can be written as:
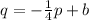
where
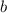 is the initial value or the y-intercept.
is the initial value or the y-intercept.
Using the point
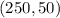
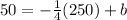
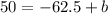
Adding 62.5 both sides.
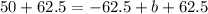
∴
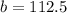
So,