Answer:
100 children
Explanation:
Let x, y, and z denote the number of children, students, and adults, respectively.
A theater has a seating capacity of 750
So,
 ---A
---A
Theater charges $2 for children, $4 for students, and $6 for adults.
Cost for x children = 2x
Cost for y students = 4y
Cost for y adults = 6z
The receipts totaled $3300
So,
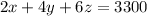 ---B
---B
Now we are given that there were half as many adults as children and students combined.
So,
 ---C
---C
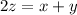
Substitute the value of x+y in A
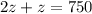
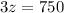
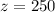
Substitute the value of z in A and B
In A
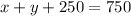
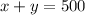 ---D
---D
In B
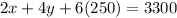
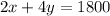 ---E
---E
Solve D and E
Substitute the value of x from D in E
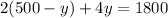
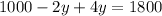
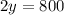
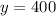
Substitute the value of y in D
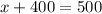
x=100
Hence 100 children attended the show