Question

The radius of the aorta is ~ 10 mm = 10-2 m and the blood flowing through it has a speed ~ 300 mm/s = 0.3 m/s. A capillary has a radius ~ 4×10-3 mm = 4×10-6 m, but there are literally billions of them. The average speed of blood through the capillaries is ~ 5×10-4 m/s. (i) Calculate the effective cross sectional area of the capillaries and (ii) the approximate number of capillaries.

Answer 1

0.00188 m²

37500000

Step-by-step explanation:

`A_2` = Area of aorta

Radius of aorta = 0.01 m

`v_2` = Velocity of blood through aorta = 0.3 m/s

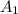`A_1` = Area of capillaries

`v_1` = Velocity of blood through capillaries =
`5* 10^(-4)\ m/s`

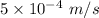
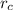`r_c` = Radius of capillaries =
`4* 10^(-6)\ m`

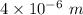
From continuity equation as the mass is conserved

`A_1v_1=A_2v_2\\\Rightarrow A_1=(A_2v_2)/(v_1)\\\Rightarrow A_1=(\pi (10^(-3))^2* 0.3)/(5* 10^(-4))\\\Rightarrow A_1=0.00188\ m^2`

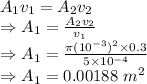
Effective cross sectional area of the capillaries is 0.00188 m²

Area of capillaries is also given by

`A_1=N* \pi r_c^2\\\Rightarrow N=(A_1)/(\pi r_c^2)\\\Rightarrow N=((\pi (10^(-3))^2* 0.3)/(5* 10^(-4)))/(\pi* (4* 10^(-6))^2)\\\Rightarrow N=37500000`

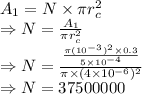
The number of capillaries is 37500000