Answer:
0.2389
Explanation:
The amount of warpage in a type of wafer used in the manufacture of integrated circuits has mean 1.3 mm and standard deviation 0.1 mm.
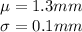
A random sample of 200 wafers is drawn
we are supposed to find What is the probability that the sample mean warpage exceeds 1.305 mm
We will use central limit theorem
According to central limit theorem:
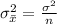


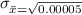
Now we are supposed to find What is the probability that the sample mean warpage exceeds 1.305 mm i.e.P(x>1.305)

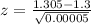
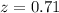
Refer the z table
P(z<0.71)=0.7611
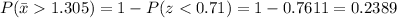
Hence the probability that the sample mean warpage exceeds 1.305 mm is 0.2389