Answer: 0.9726
Explanation:
Let x be the random variable that represents the distance the tires can run until they wear out.
Given : The top-selling Red and Voss tire is rated 50,000 miles, which means nothing. In fact, the distance the tires can run until they wear out is a normally distributed random variable with a
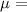 67,000 miles and a
67,000 miles and a
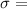 5,200 miles.
5,200 miles.
Then , the probability that a tire wears out before 60,000 miles :
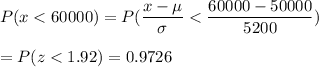 [using p-value table for z]
[using p-value table for z]
Hence, the probability that a tire wears out before 60,000 miles= 0.9726