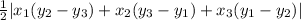Question

A graph passes through the points (0,2), (2,6), and (3,12)). Does this graph represent a linear function or a nonlinear function explain your answer in words

Answer 1

The graph of the function is nonlinear.

Explanation:

If the points (0,2), (2,6) and (3,12) lie on the same straight line then the area of the triangle formed by those points will be zero.

So, we have to find the area of a triangle formed by those points and if we get the area to be zero, then only the graph though the above points will represent a linear function otherwise the graph will be nonlinear.

Now, area Δ =
`(1)/(2)  |0(6-12)+ 2(12-2)+ 3(2-6)|`

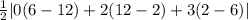
= 4 sq. units ≠ 0

Hence, the graph of the function is nonlinear. (Answer)

We know, that the area of the triangle formed by the points (
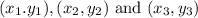`(x_(1). y_(1)), (x_(2), y_(2)) \textrm{ and } (x_(3), y_(3))` is given by

Δ =
`(1)/(2)  |x_(1)(y_(2)-y_(3))+x_(2)(y_(3)-y_(1))+ x_(3)(y_(1)-y_(2)) |`