Question

A police officer claims the proportion of drivers using cell phones while driving 35%. To test this claim, a random sample of drivers are monitored and checked if are using a cell phone while driving Assume that the test statistic for this hypothesis test is −2.48. Since this is a two tailed hypothesis test, assume that the critical values for this hypothesis test are −2.576 and 2.576. Come to a decision for the hypothesis test and interpret your results with respect to the original claim

Answer 1

Answer with explanation:

Let p be the population proportion of the drivers using cell phones while driving.

Given : A police officer claims the proportion of drivers using cell phones while driving 35%.

i.e.
`p=0.35`

To test this claim, a random sample of drivers are monitored and checked if are using a cell phone while driving.

Then, the appropriate hypothesis would be :-

`H_0: p=0.35\\\\ H_a:p\\eq0.35`

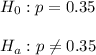
∵ Alternative hypothesis is two-tailed , so the test is a two-tailed test.

Also, it is given that the test statistic for this hypothesis test is −2.48.

`z_(calc)=-2.48`

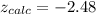
Since this is a two tailed hypothesis test, assume that the critical values for this hypothesis test are −2.576 and 2.576.

Here, -2.576< -2.48< 2.576

`\Rightarrow\-2.576< z_(calc)< 2.576`

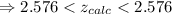
So we failed to reject the null hypothesis
`H_0` .

Interpretation: We have sufficient evidence to support the claim that proportion of drivers using cell phones while driving 35%.