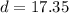Answer:
Rounding it to two decimal places, we get distance,
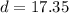
Explanation:
Given:
The two points are
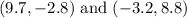
The distance between the two points can be obtained using the distance formula which is given as:
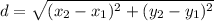
Here, for the points,
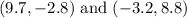
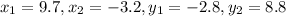
Therefore, the distance between the points is:
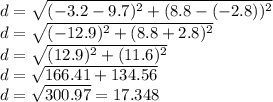
Rounding it to two decimal places, we get